Question

An elevator whose mass is m = 400 kilograms is supported by a cable. A frictional force of f = 80 newtons is applied to the elevator as it moves. Determine the tension T in the cable when the elevator is:

a.) Stationary;
b.) Moving upward while accelerating at 2.8 m/s2;
c.) Moving upward with a constant velocity-magnitude of 5 m/s;
d.) Accelerating downward at 2.8 m/s2 with velocity downward;
e.) Moving downward with a constant velocity-magnitude of 5 m/s.

Answer 1

3924 N

5124 N

4004 N

2884 N

4004 N

Step-by-step explanation:

m = Mass of elevator = 400 kg

g = Acceleration due to gravity = 9.81 m/s²

a = Acceleration

f = Friction force = 80 N

When the elevator is stationary only the acceleration due to gravity will be acting on it

Tension

`T=mg\\\Rightarrow T=400* 9.81\\\Rightarrow T=3924\ N`

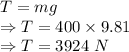
The tension is 3924 N

The balanced force equation would be

`T-mg-f=ma\\\Rightarrow T=ma+mg+f\\\Rightarrow T=400* 2.8+400* 9.81+80\\\Rightarrow T=5124\ N`

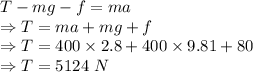
The tension is 5124 N

When velocity is constant acceleration is zero

`T-mg-f=0\\\Rightarrow T=mg+f\\\Rightarrow T=400* 9.81+80\\\Rightarrow T=4004\ N`

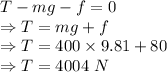
The tension is 4004 N

`T-mg-f=-ma\\\Rightarrow T=-ma+mg+f\\\Rightarrow T=-400* 2.8+400* 9.81+80\\\Rightarrow T=2884\ N`

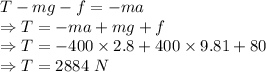
The tension would be 2884 N

When velocity is constant acceleration is zero

`T-mg-f=0\\\Rightarrow T=mg+f\\\Rightarrow T=400* 9.81+80\\\Rightarrow T=4004\ N`

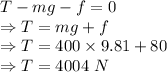
The tension is 4004 N