Question

Let a be the vector of length 125 that when drawn in standard position makes a 144° angle with the positive x-axis. Let b be the vector of length 39 that when drawn in standard position makes a 302° angle with the positive x-axis. Find the length of v = a + b and the angle θ that v makes with the positive x-axis when drawn in standard position. Round your approximations to three decimal places.

Answer 1

The length is 90.033 and the angle that v makes with the positive x-axis is 153.339°

Explanation:

Firstly we will have to convert our given vectors to their rectangular Cartesian vector form as follow,

`a=125(icos(144)+jsin(144))=-101.127i+73.473j\\b=39(icos(302)+jsin(302))=20.667i-33.074j`

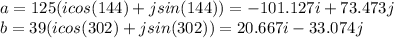
Now that we have these, we can add them to obtain v as follows,

`v=a+b\\v=-80.46i+40.399j`

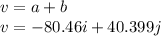
Now that we have the Cartesian vector form we can calculate its length and its direction with respect to the positive x-axis as follows(In fact we usually refer the angles from the positive x-axis),

`|v|=\sqrt{80.46^(2)+40.399^(2)}=90.033\\ angle(v)=tan^(-1)(40.399/(-80.46))=153.339`

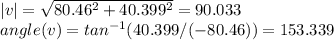
So the length of the vector is 90.033 and the angle it makes with the positive x-axis is 153.339°.