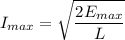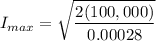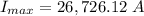Answer:
(a)
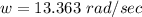
(b)
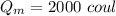
(c)
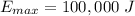
(d)
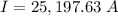
(e)
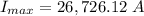
Step-by-step explanation:
LC Circuit
The dynamics of an LC circuit is explained as the energy stored in the capacitor C in the form of an electrical field is transferred to the inductor L as a magnetic field. The energy stored in a capacitor is
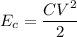
Where V is the potential between its plates where a charge Q is stored. The relation between them is
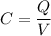
The energy stored in an inductor of self-inductance L is
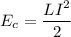
Where I is the current flowing through the inductor. If we apply the principle of conservation of energy, the loss of electric energy in the capacitor will transform into magnetic energy in the inductor and vice-versa.
The angular frequency of oscillation of a LC circuit is
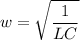
The question provides the following data
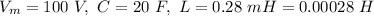
(a) The angular frequency is
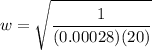
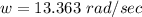
(b) When the voltage is at maximum, the charge will also be maximum, its value can be computed solving for Q
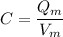
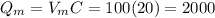
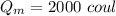
(c) At t=0, the voltage is at maximum, so the energy stored is

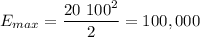
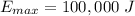
(d) If the charge reaches 1/3 of the initial value, it means 2/3 of the charge were transformed in magnetic energy. Let's call
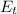 to the transferred electric energy to magnetic energy, and
to the transferred electric energy to magnetic energy, and
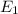 to the remaining electric energy in the capacitor. Knowing
to the remaining electric energy in the capacitor. Knowing
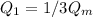
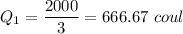
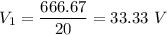
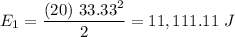
The energy transfered is
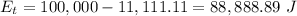
We can compute the current solving for I in:
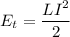
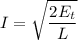
Calculating I
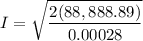
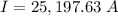
(e) To find
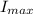 , we'll assume all the electric energy is transformed to magnetic, so
, we'll assume all the electric energy is transformed to magnetic, so