Answer:
a)
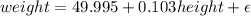
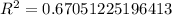

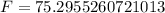
b) H0:
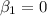
H1:
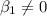
On this case the test statistc is given by
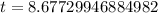
And the p value obtined was:
 and since the p value is lower than th significance level we can reject the null hypothesis at 5% of significance. The slope is significant.
and since the p value is lower than th significance level we can reject the null hypothesis at 5% of significance. The slope is significant.
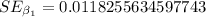
Explanation:
We assume the following info:
Gender Height Weight
Male 73.84701702 241.8935632
Male 68.78190405 162.3104725
Male 74.11010539 212.7408556
Male 71.7309784 220.0424703
Male 69.88179586 206.3498006
Male 67.25301569 152.2121558
Male 68.78508125 183.9278886
Male 68.34851551 167.9711105
Male 67.01894966 175.9294404
Male 63.45649398 156.3996764
Male 71.19538228 186.6049256
Male 71.64080512 213.7411695
Male 64.76632913 167.1274611
Male 69.2830701 189.4461814
Male 69.24373223 186.434168
Male 67.6456197 172.1869301
Male 72.41831663 196.0285063
Male 63.97432572 172.8834702
Male 69.6400599 185.9839576
Male 67.93600485 182.426648
Male 67.91505019 174.1159291
Male 69.43943987 197.7314216
Male 66.14913196 149.173566
Male 75.20597361 228.7617806
Male 67.89319634 162.0066518
Male 68.1440328 192.3439766
Male 69.08963143 184.4351744
Male 72.80084352 206.8281894
Male 67.42124228 175.2139224
Male 68.49641536 154.3426389
Male 68.61811055 187.5068432
Male 74.03380762 212.9102253
Male 71.52821604 195.0322432
Male 69.1801611 205.1836213
Male 69.57720237 204.1641255
Male 70.4009288 192.9035151
Male 69.07617117 197.4882426
Male 67.19352328 183.8109732
Male 65.80731565 163.8518249
And we can use excel to solve the problem
Part a
On this case we need to click on Data>Data analysis>Regression>Ok
We select the input Y range and th X range and then we click in Ok.
The output obtained is on the first figure attached.
And in order to estimate the regression line we need to look into the column Coefficients, and for this case we got:
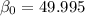
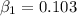
And the linear model would be given by:
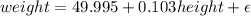
For the determination coefficient we have:
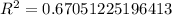
And the adjusted
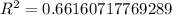
And if we analyze the output th F statistic is given by:
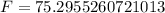
Part b
We want to test:
H0:
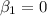
H1:
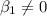
On this case the test statistc is given by
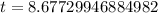
And the p value obtined was:
 and since the p value is lower than th significance level we can reject the null hypothesis at 5% of significance. The slope is significant.
and since the p value is lower than th significance level we can reject the null hypothesis at 5% of significance. The slope is significant.
The standard error for the slope is given in the output:
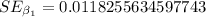
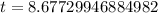

We reject the null hypothesis.