Answer:
(a)
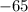
(b)
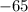
Explanation:
We have been a function
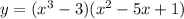 . We are asked to find the instantaneous rate of change of the function and the slope of the tangent line at point
. We are asked to find the instantaneous rate of change of the function and the slope of the tangent line at point
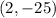 .
.
(a) First of all, we will find the derivative of our given function using product rule.


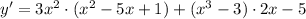
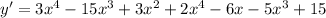

Now, we will substitute
 in our derivative function to find slope of tangent line as:
in our derivative function to find slope of tangent line as:
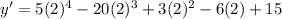
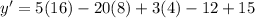
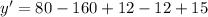

Therefore, the slope of the tangent line is -65 at point
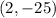 .
.
(b) We know that instantaneous rate of change of the function at a point is equal to the derivative of the function at that point.
We already figured it out that derivative of our given function at
 is
is
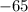 , therefore, the instantaneous rate of change of the function is also
, therefore, the instantaneous rate of change of the function is also
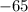 at point
at point
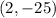 .
.