Answer:
1,200V/m
Step-by-step explanation:
I will call the first point A and the second point B, we have:
voltage in A:
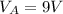
Voltage in B:
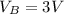
The distance between the points:
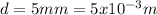
And we calculate the electric field due to the difference of potential as follows:
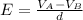
Substituting known values:
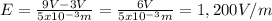
the strength of the electric field between these points 1,200V/m