Question

Queue at Park Vehicles arrive at an entrance to a recreational park. There is a single gate, where a park attendant distributes a free brochure. The park opens at 8:00 A.M., at which time vehicles begin to arrive at an average rate of 180 veh/h (Poisson distributed). Assume it takes an average of 15 seconds to distribute brochures, but the distribution time varies depending on whether the park patrons have questions related to park operating policies or not. Compute the: A. What is the average length of queue, not including the vehicle being served? B. Estimate the average waiting time of a vehicle? C. What is the average total time spent in the queue? D. What is the probability that there are 3 or more vehicles at the queue? E. What is the probability of a vehicle spending more than 1.5 min in the queue?

Answer 1

Step-by-step solutions given below

Step-by-step explanation:

We are given the following parameters:

Average arrival rate, λ = 180 veh/h

Average service time = 15 seconds

Therefore, the service rate, μ is given by 1/time = 1/15 veh/second

Converting to veh/hour, we simply multiply veh/second by (60*60) = 3600

Hence μ = (1/15)*3600 = 240 veh/hr

(A) Average length of queue = λ^2/μ(μ - λ)

Hence, we have

Here, k = 3

Hence, substituting the values, we have

=
`(180/240)^3+1`

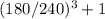
= 0.3164*100

= 31.64%