Answer:
The induced emf can be found by Faraday’s Law.
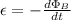
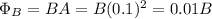
The magnetic field is increasing at a rate of 0.1T/s. So,

Finally,
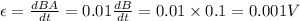
Explanation:
Faraday’s Law states that a change in the magnetic flux induces an emf in the circuit. The magnetic flux is the multiplication of magnetic field and the area of the loop. The area of the loop is simple, and the change of magnetic field as a function of time is given in the question.
The minus sign in front of the Faraday’s Law means that the induced current always opposes the change of the magnetic flux. Since we do not know the direction of the magnetic field in this question, we cannot find the direction of the induced emf on the loop.