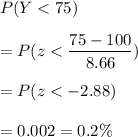Question

A group of married couples takes an IQ test. The average husband's IQ is 105 with an SD of 15 and the average wife's IQ is 110 with an SD of 10. The correlation between husband's and wife's IQ is 0.5.

a) A man has an IQ of 75, what would you predict his wife's IQ is?
b) Of all men with an IQ of 75, about what percent are smarter than their wives?

Answer 1

Wife' s IQ = 100

0.2% are smarter than their wives.

Explanation:

We are given the following information in the question:

Husband:

Mean = 105

SD = 15

Wife:

Mean = 110

SD = 10

Correlation between husband's and wife's IQ = 0.5

a) Let the husbands be represented by X and wives by Y.

Man's IQ = 75

Standardizing the scores, we get:

Formula:

`z_(score) = \displaystyle(x-\mu)/(\sigma)`

`(75-105)/(15) = -2`

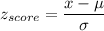
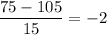
We know that if we standardize our scores then:

`Z_Y = rZ_X`

Putting value, we get:

`Z_Y = 0.5(-2) = -1`

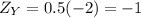
So,

`Y = 110 + (-1)*10 = 100`

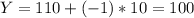
b) Standard deviation of IQ's of wives married to husbands with IQ of 75 is:

`SD = SD_Y√(1-r^2) = 10√(1-0.25) = 8.66`

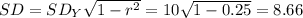
We know that a husband of an IQ 75 will have a wife of a mean IQ of 100. So for a man to be smarter than his wife she should have IQ less than 75.

`P(Y<75)\\\\=P(z<\displaystyle(75-100)/(8.66))\\\\=P(z<-2.88)\\\\= 0.002 = 0.2\%`