Answer:
2123.55 $/hr
Step-by-step explanation:
Given parameters are:
 KV
KV
L = 143 km
I = 500 A
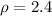
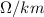
So, we will find the voltage potential provided for the city as:
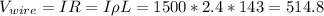 kV
kV
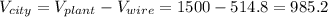 kV
kV
Then, we will find dissipated power because of the resistive loss on the transmission line as:
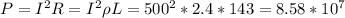 W
W
Since the charge of plant is not given for electric energy, let's assume it randomly as

Then, we will find the price of energy transmitted to the city as:
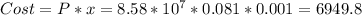 $/hr
$/hr
To calculate money per hour saved by increasing the electric potential of the power plant:
Finally,
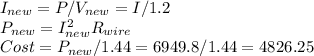 $/hr
$/hr
The amount of money saved per hour =
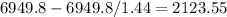 $/hr
$/hr
Note: For different value of the price of energy, it just can be substituted in the equations above, and proper result can be found accordingly.