Question

Let L1 be the line passing through the points Q1(−4, 4, 3) and Q2(0, 10, 1) and let L2 be the line passing through the point P1(3, 20, 0) with direction vector d=[3, −1, −2]T. Determine whether L1 and L2 intersect. If so, find the point of intersection Q.

Answer 1

L1 and L2 do not intersect.

Explanation:

I am saying that the first line has the initial point Q1 and passes through the vector Q2 - Q1.

Q2 - Q1 = (0,10,1) - (-4,4,3) = (4,6,-2).

So the parametric equations for L1 are:

`x(t) = -4 + 4t`

`y(t) = 4 + 6t`

`z(t) = 3 - 2t`

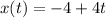
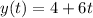
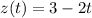
For L2, we already have a point and the vector, so we can build the parametric equations:

`x(t) = 3 + 3t`

`y(t) = 20 - t`

`z(t) = 0 - 2t`

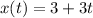
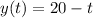
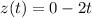
Now we must find the value of t for which x,y and z are equal. If all are equal at the same time t, these lines intersect at this instant of time.

So

x

`-4 + 4t = 3 + 3t`

`t = 7`

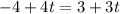
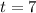
y

`4 + 6t = 20 - t`

`7t = 16`

`t = 2....`

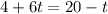
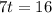
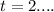
Since the value of t when x are equal is different to when y are equal, these lines do not intersect.