Answer:
b
Explanation:
Minimum sample size for estimating the population proportion of pine trees over 90 years old in a forest near where you live with margin of error no more than 2% can be calculated using the equation:
n≥ p×(1-p) ×
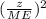 where
where
- p is the proportion of pine trees over 90 years old in a forest near where you live
- z is the corresponding z-score for the confidence level
- ME is the margin of error in the estimation (2% or 0.02)