Question

A system consists of two spheres, of mass m and 2m, connected by a rod of negligible mass, as shown above. The system is held at its center of mass with the rod horizontal and released from rest near Earth's surface at time t = 0.

Answer 1

Rod will remain horizontal all the time after release.

Step-by-step explanation:

This is because net torque on the rod about any point in space is zero.

Let assume that distance between the two masses m and 2m is L.

Also m is situated at origin and in positive XY direction.

Then , Center of mass is at L(
`\frac{mx_(1)+2mx_(2)} }{m +2m}`)

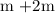COM =
`(2L)/(3)`

So let us calculate net torque about hinged point which COM.

• Torque because of hinge force is zero because it passes from that point itself.
• Torque on 2m mass is 2mg(L/3) in nenegative Z direction.
• Torque on m mass is mg(2L/3) in positive Z direction.

As both torque are equal and opposite then net torque =0.

Thus it got balanced.