Question

Suppose an airline policy states that all baggage must be box-shaped with a sum of length, width, and height not exceeding 108in. What are the dimensions and volume of a square based box with the greatest volume under these conditions?

Answer 1

Length = Width = Height =36 inches

Volume =46,656 cubic inches

Explanation:

Let

x ----> the length of the box-shaped in inches

y ----> the width of the box-shaped in inches

z ---> the height of the box shaped in inches

we know that

`x+y+z=108`

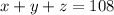
`z=108-x-y` ----> equation A

Remember that

we have a square based box

so

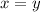`x=y` ----> equation B

substitute equation B in equation A

`z=108-x-x`

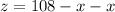
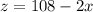`z=108-2x` ----> equation C

The volume of the box is equal to

`V=xyz` ----> equation D

substitute equation B and equation C in equation D

`V=x(x)(108-2x)`

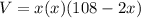
solve for x

`V=-2x^3+108x^2`

Since we're looking for a maximum, that will happen when the slope of the above equation is 0. And the first derivative will give us that slope.

so

calculate the first derivative

`V'=-6x^2+216x`

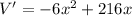
equate to zero

`-6x^2+216x=0`

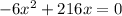
solve for x

Factor -6x

`-6x(x-36)=0`

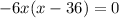
The solutions are

x=0, x=36 in

Find the value of y

`y=x`

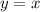
so

`y=36\ in`

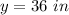
Find the value of z

`z=108-2(36)`

`z=108-72=36\ in`

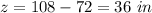
therefore

The dimensions are 36 in by 36 in by 36 in

The volume is equal to

`V=(36)(36)(36)=46,656\ in^3` ----> is a cube