Question

A reaction A(aq)+B(aq)↽−−⇀C(aq) has a standard free‑energy change of −4.51 kJ/mol at 25 °C.

What are the concentrations of A, B, and C at equilibrium if, at the beginning of the reaction, their concentrations are 0.30 M, 0.40 M, and 0 M, respectively?

How would your answers change if the reaction had a standard free-energy change of +4.51 kJ/mol?

A. All concentrations would be lower.
B. There would be more A and B but less C.
C. There would be less A and B but more C.

How would your answers change if the reaction had a standard free-energy change of +4.51 kJ/mol?

A. All concentrations would be lower.
B. There would be more A and B but less C.
C. There would be less A and B but more C.
D. There would be no change to the answers.
E. All concentrations would be higher.

Answer 1

(a) [A] = 0.13 M, [B]= 0.23 M and [C] = 0.17 M.

(b) Option B.

Step-by-step explanation:

The reaction given:

A(aq) + B(aq) ⇄ C(aq) (1)

Initial: 0.30M 0.40M 0M (2)

Equilibrium: 0.3 - x 0.4 - x x (3)

The equation of Gibbs free energy of the reaction (1) is the following:

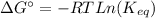`\Delta G^(\circ) = - RTLn(K_(eq))` (4)

where ΔG°: is the Gibbs free energy change at standard conditions, R: is the gas constant, T: is the temperature and
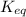`K_(eq)`: is the equilibrium constant

(a) To calculate the concentrations of A, B, and C at equilibrium, we need first determinate the equilibrium constant using equation (4), with ΔG°=-4.51x10³J/mol, T=25 + 273 = 298 K, R=8.314 J/K.mol:

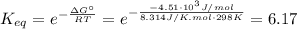`K_(eq) = e^{-(\Delta G^(\circ))/(RT)} = e^{-(-4.51\cdot 10^(3) J/mol)/(8.314 J/K.mol \cdot 298 K)} = 6.17` (5)

Now, we can calculate the concentrations of A, B, and C at equilibrium using the equilibrium constant calculated (5):

`K_(eq) = ([C])/([A][B]) = (x)/((0.3 - x)(0.4 - x))` (6)

Solving equation (6) for x, we have two solutions x₁=0.69 and x₂=0.17, and by introducing the solution x₂ into equation (3) we can get the concentrations of A, B, and C at equilibrium:

`[A] = 0.3 - x_(2) = 0.3 - 0.17 = 0.13 M`

`[B] = 0.4 - x_(2) = 0.4 - 0.17 = 0.23 M`

`[C] = x = 0.17 M`

Notice that the solution x₁=0.69 would have given negative values of the A and B concentrations.

(b) If the reaction had a standard free-energy change of +4.51x10³J/mol, the equilibrium constant would be:

`K_(eq) = e^{-(\Delta G^(\circ))/(RT)} = e^{-(4.51\cdot 10^(3) J/mol)/(8.314 J/K.mol \cdot 298 K)} = 0.16`

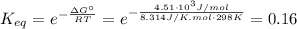
By solving the equation (6) for x, with the equilibrium constant calculated, we can get again two solutions x₁ = 6.9 and x₂= 0.017, and by introducing the solution x₂ into equation (3) we can get the concentrations of A, B, and C at equilibrium:

`[A] = 0.3 - x_(2) = 0.3 - 0.017 = 0.28 M`

`[B] = 0.4 - x_(2) = 0.4 - 0.017 = 0.38 M`

`[C] = x = 0.017 M`

Again, the solution x₁=6.9 would have given negative values of the A and B concentrations.

Hence, the correct answer is option B: there would be more A and B but less C.

I hope it helps you!