Answer:
0.47%.
Explanation:
We have been given that a research student measured the age of an ice layer at 70 m depth as 425 years. The accepted value reported is 427 years.
We will use error percent formula to solve our given problem.
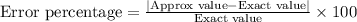
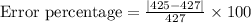
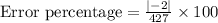
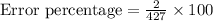
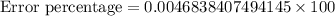
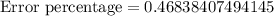
Rounding to two decimal places:
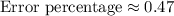
Therefore, the percent error of students value is approximately 0.47%.