Question

A tank having a capacity of 100 gallons is half full of fresh water. A pipe is open that lets treated sewage enter the tank at a rate of 4 gal/min. At the same time, a drain is open to allow the mixture to leave the tank at a rate of 2 gal/min. If the treated sewage contains 10 grams of usable potassium per gallon, what is the concentration of potassium in the tank when it is full?

Answer 1

Answer: 2.4 grams/gal.

Explanation:

This question can be considered as the mathematical modeling of a tank. The key point here is the concentration has to diminish gradually as the time passes. The water exiting the tank must include some ratio of the potassium added. Thus, a common mistake would be assuming the exit flow as pure water. We should structure a logical model as the following:

The volume of water in the tank (V-total)= Change in volume in a minute (İnlet flow - exit flow) + initial volume (50 gal). This is equal to (4 gal/min - 2 gal/min) + 50 gal= 50 gal + 2gal/min*t where t represents time in minutes and the representation will be V-tot= 50 + 2*t

Next, we have to calculate the amount and the change of pottassium per unit time. We know that 10 grams of potassium is introduced in each minute to the tank. However, some amount in proportion to the exit flow will leave as potassium will totally dissolve in the water (and we should assume that it will dissolve homogeneously as soon as it is introduced). Thus, at a certain time, the total amount of potassium introduced will be 10 grams*t. The amount of potasium leaving will be in proportion to exit flow and total time. The leaving potassium amount can be modelled as (2 gal/min)/V-tot*10 grams*t. (2 gal/min)/V-tot term represents the ratio of leaving amount of potassium and 10 grams*t is introduced so when it is multiplied by the ratio, we will have the exact amount left at a certain time. Thus, the weight term is 10 grams*t-(2 gal/min)/V-tot*10 grams*t.

The concentration formula is weight/volume. Thus the concentration at a certain time will be
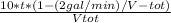`(10*t*(1-(2 gal/min)/V-tot))/(Vtot)` when the weight term is taken in a common t parenthesis.

Now, we have to calculate how much time it would take for a tank to be filled. The total capacity is 100 gallons and at the beginning, where is only 50 gallons. Thus, we have to calculate the amount of time required for another 50 gallons to accumulate in the tank. We know that 2 gallons are accumulated in the tank per minute, thus at t=25 the tank will be full. So, in the formula we have to insert 25 for t.

V-tot at t=25 is 100 gallons since the tank will be full. Thus, inserting t=25 and V-tot is 100, we get the result 2.4 grams/gal.