Answer:
19.81m/s
Step-by-step explanation:
To find the speed at which the car leaves the cliff, first we need to know how long it took to reach the ground. We do this with the equation:
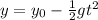
Where
 is the vertical position at a time
is the vertical position at a time
 , since we are looking for the moment when the car reaches the gound:
, since we are looking for the moment when the car reaches the gound:
 .
.
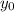 is the initial vertical position, in this case the height of the cliff:
is the initial vertical position, in this case the height of the cliff:
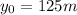 .
.
 is gravitational acceleration:
is gravitational acceleration:
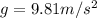 .
.
So replacing the known values:
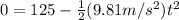
and since we need the time, we clear for it:

At time
 the car reaches the gound, according to the problem at a horizontal distance from the base of the cliff of 100m.
the car reaches the gound, according to the problem at a horizontal distance from the base of the cliff of 100m.
To find the velocity we use:

where
 is the horizontal distance at time
is the horizontal distance at time
 (in this case
(in this case
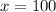 and
and
 ),
),
 is the initial horizontal distance, we define the cliff as zero in horizontal distance so
is the initial horizontal distance, we define the cliff as zero in horizontal distance so
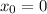 , and
, and
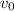 is the velocity of the car when it rolled of the cliff.
is the velocity of the car when it rolled of the cliff.
replacing the known values:

and we clear for
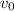 :
:
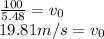
The initial velocity (when it rolled of the cliff) is 19.81m/s