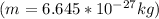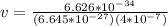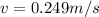Question

What would the speed of each particle be if it had the same wavelength as a photon of violet light ( λ = 400.0 nm ) ?

a. proton ( mass = 1.673 × 10 − 24 g ) speed: m / s
b. neutron ( mass = 1.675 × 10 − 24 g ) speed: m / s
c. electron ( mass = 9.109 × 10 − 28 g ) speed: m / s
d. alpha particle ( mass = 6.645 × 10 − 24 g ) speed:

Answer 1

To develop this problem we will use the DeBroglie relationship for which the wavelength is considered as

`\lambda = (h)/(mv)`

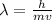
Where,

h = Planck's constant

m = mass

v = Velocity

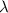`\lambda` = Wavelength

Rearranging the equation we have that the speed would be

`v = (h)/(m\lambda)`

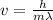
Our given values are considered

`\lambda = 400nm = 4*10^(-7)m`

`h = 6.626*10^(-34) J\cdot s`

`m = 1.673*10^(-24)g = 1.673*10^(-27)kg`

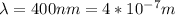
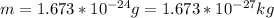
The value of the mass varies, therefore its speed would be given as:

Proton
`(m=1.673*10^(-27)kg)`

`v = (6.626*10^(-34))/((1.673*10^(-27))(4*10^(-7)))`

`v = 0.99m/s`

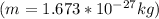
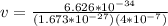
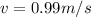
Neutron
`(m=1.675*10^(-27)kg)`

`v = (6.626*10^(-34))/((1.675*10^(-27))(4*10^(-7)))`

`v = 0.988m/s`

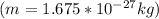
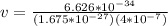
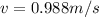
Electron
`(m=9.109*10^(-31)kg)`

`v = (6.626*10^(-34))/((9.109*10^(-31))(4*10^(-7)))`

`v = 1818.53m/s`

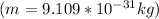
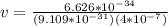
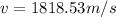
Alpha particle
`(m=6.645*10^(-27) kg)`

`v = (6.626*10^(-34))/((6.645*10^(-27) )(4*10^(-7)))`

`v = 0.249m/s`