Question

A 20-volt electromotive force is applied to an LR-series circuit in which the inductance is 0.1 henry and the resistance is 30 ohms. Find the current i(t) if i(0) = 0.

Answer 1

`i(t)=(2/3)(1-e^(-300t))`

Explanation:

Before we even begin it would be very helpful to draw out a simple layout of the circuit. Then we go ahead and apply kirchoffs second law(sum of voltages around a loop must be zero) on the circuit and we obtain the following differential equation,

`-V +Ldi/dt+Ri=0`

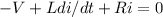
where V is the electromotive force applied to the LR series circuit, Ldi/dt is the voltage drop across the inductor and Ri is the voltage drop across the resistor. we can re write the equation as,

`di/dt+Ri/L=V/L`

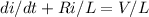
Then we first solve for the homogeneous part given by,

`di/dt+Ri/L=0`

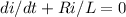
we obtain,

`i(t)_(h) =I_(max)e^(-Rt/L)`

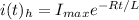
This is only the solution to the homogeneous part, The final solution would be given by,

`i(t)=i(t)_(h) +c`

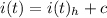
where c is some constant, we added this because the right side of the primary differential equation has a constant term given by V/R. We put this in the main differential equation and obtain the value of c as c=V/R by comparing the constants on both sides.if we put in our initial condition of i(0)=0, we obtain
`I_(max) =V/R`, so the overall equation becomes,

`I(t)=(V/R)(1-e^(-Rt/L))`

where if we just plug in the values given in the question we obtain the answer given below,

`i(t)=(2/3)(1-e^(-300t))`