Answer:
A, B and F are the right answers
Step-by-step explanation:
The formula is
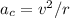
A) Increasing both the radius and the speed by a factor of 9
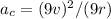 =
=
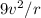
which means the acceleration will increase by a factor of 9
B) Keeping the speed fixed and decreasing the radius by a factor of 9
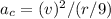 =
=
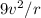
which means the acceleration will increase by a factor of 9
C) Keeping the radius fixed and increasing the speed by a factor of 9
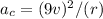 =
=
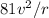
It will increase the acceleration 81 times
D) Keeping the speed fixed and increasing the radius by a factor of 9
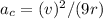 =
=
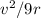
It will decrease the acceleration by 9 times
E) decreasing both the radius and the speed by a factor of 9
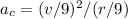 =
=
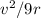
It will decrease the acceleration by 9 times
F) Keeping the radius fixed and increasing the speed by a factor of 3
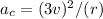 =
=
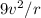
It will increase the acceleration by 9 times