Question

Find the arc-length parametrization of the curve that is the intersection of the elliptic cylinder x 2 + y 2/2 = 1 and the plane z = x−2. Use s as the arc-length parameter with s = 0 corresponds to the point (1, 0, −1). Specify the limits for s.

Answer 1

`f(\theta) = (cos((\theta)/(\sqrt2)), \sqrt2 sin((\theta)/(\sqrt2)), cos((\theta)/(\sqrt2))-2)`

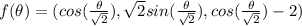
0 ≤ Ф ≤ 4π.

Explanation:

since x²+y²/2 = 1, then x²+s² = 1, with s = (y/√2)². Hence, (x,s) = (cos(Ф),sin(Ф)) and (x,y,z) = (cos(Ф),√2 sin(Ф), cos(Ф)-2). This expression evaluated in zero gives as result (1,0,-1). The derivate of this function is (-sin(Ф),√2 cos(Ф), -sen(Ф))

the norm of the derivate is √(sin²(Ф) + 2cos²(Ф)+sin²(Ф)) = √2. In order to make the norm equal to 1, i will divide Ф by √2, so that a √2 is dividing each term after derivating.

We take

`f(\theta) = (cos((\theta)/(\sqrt2)), \sqrt2 sin((\theta)/(\sqrt2)), cos((\theta)/(\sqrt2))-2)`

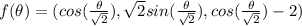
Note that

• 
  `f(0) = (1,0,-1)`
• 
  `f'(\theta) = ((sin((\theta)/(\sqrt2)))/(\sqrt2), cos((\theta)/(\sqrt2))}, (sin((\theta)/(\sqrt2)))/(\sqrt2))`

Whose square norm is 1/2cos²(Ф/2)+sen²(Ф/2)+1/2cos²(Ф/2) = 1. This is te parametrization that we wanted.

The values from Ф range between 0 an 4π, because the argument of the sin and cos is Ф/2, not Ф, Ф/2 should range between 0 and 2π.