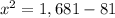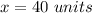Question

Find x. Assume that segments that appear tangent are tangent.

Answer 1

`x=40\ units`

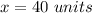
Explanation:

see the attached figure to better understand the problem

we know that

segment BC is a tangent to the circle at point B ---> given problem

AB is a radius of the circle

The tangent BC is perpendicular to the radius AB

Remember that

According to the Perpendicular Tangent Theorem, tangent lines are always perpendicular to a circle's radius at the point of intersection

so

The triangle ABC is a right triangle

Applying the Pythagorean Theorem

`AC^2=AB^2+BC^2`

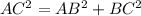
substitute the given values

`41^2=9^2+x^2`

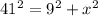
solve for x

`1,681=81+x^2`

`x^2=1,681-81`

`x=40\ units`