Answer:
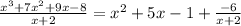
So the quotient is
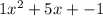 and the remainder is
and the remainder is
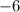 .
.
Explanation:
We could do this by synthetic division since the denominator is a linear factor in the form
 .
.
Since we are dividing by
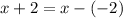 , this is our setup for the synthetic division:
, this is our setup for the synthetic division:
-2 | 1 7 9 -8
| -2 -10 2
______________
1 5 -1 -6
So the quotient is
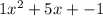 and the remainder is
and the remainder is
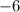 .
.
So
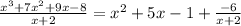 .
.
We can also do long division.
x^2+5x-1
____________________
x+2| x^3+7x^2+9x-8
-(x^3+2x^2)
-------------------
5x^2+9x-8
-( 5x^2+10x)
--------------------
-x-8
-(-x-2)
--------------
-6
So we see here we get the same quotient,
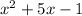 . and the same remainder,
. and the same remainder,
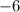 .
.
Now let's check our result that:
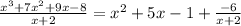 .
.
So I'm going to rewrite the right hand side as a single fraction:
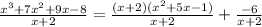 .
.
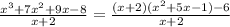
Now let's focus on multiplying
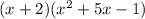 .
.
We are going to multiply the first term of the first ( ) to every term in the second ( ).
We are also going to multiply the second term of the first ( ) to every term in the second ( ).
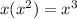
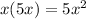
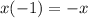
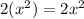
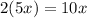
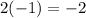
---------------------------Combine like terms:
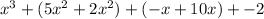
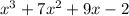
So let's go back where we were in our check of
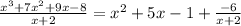 :
:
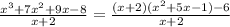
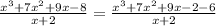
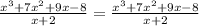
We have the exact same thing on both sides so we did good.