Question

What is the result when x^3+ 7x^2+ 9x - 8 is divided by x+ 2?

Answer 1

Explanation:

Answer 2

`(x^3+7x^2+9x-8)/(x+2)=x^2+5x-1+(-6)/(x+2)`

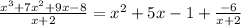
So the quotient is
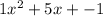`1x^2+5x+-1` and the remainder is
`-6`.

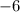Explanation:

We could do this by synthetic division since the denominator is a linear factor in the form
`x-c`.

Since we are dividing by
`x+2=x-(-2)`, this is our setup for the synthetic division:

-2 | 1 7 9 -8

| -2 -10 2

______________

1 5 -1 -6

So the quotient is
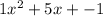`1x^2+5x+-1` and the remainder is
`-6`.

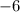So
`(x^3+7x^2+9x-8)/(x+2)=x^2+5x-1+(-6)/(x+2)`.

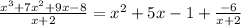We can also do long division.

x^2+5x-1

____________________

x+2| x^3+7x^2+9x-8

-(x^3+2x^2)

-------------------

5x^2+9x-8

-( 5x^2+10x)

--------------------

-x-8

-(-x-2)

--------------

-6

So we see here we get the same quotient,
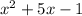`x^2+5x-1`. and the same remainder,
`-6`.

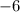Now let's check our result that:

`(x^3+7x^2+9x-8)/(x+2)=x^2+5x-1+(-6)/(x+2)`.

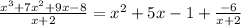So I'm going to rewrite the right hand side as a single fraction:

`(x^3+7x^2+9x-8)/(x+2)=((x+2)(x^2+5x-1))/(x+2)+(-6)/(x+2)`.

`(x^3+7x^2+9x-8)/(x+2)=((x+2)(x^2+5x-1)-6)/(x+2)`

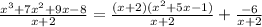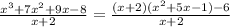
Now let's focus on multiplying
`(x+2)(x^2+5x-1)`.

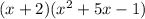We are going to multiply the first term of the first ( ) to every term in the second ( ).

We are also going to multiply the second term of the first ( ) to every term in the second ( ).

`x(x^2)=x^3`

`x(5x)=5x^2`

`x(-1)=-x`

`2(x^2)=2x^2`

`2(5x)=10x`

`2(-1)=-2`

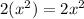
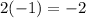
---------------------------Combine like terms:

`x^3+(5x^2+2x^2)+(-x+10x)+-2`

`x^3+7x^2+9x-2`

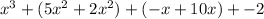
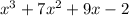
So let's go back where we were in our check of
`(x^3+7x^2+9x-8)/(x+2)=x^2+5x-1+(-6)/(x+2)`:

`(x^3+7x^2+9x-8)/(x+2)=((x+2)(x^2+5x-1)-6)/(x+2)`

`(x^3+7x^2+9x-8)/(x+2)=(x^3+7x^2+9x-2-6)/(x+2)`

`(x^3+7x^2+9x-8)/(x+2)=(x^3+7x^2+9x-8)/(x+2)`

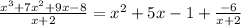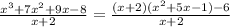
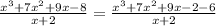
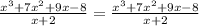
We have the exact same thing on both sides so we did good.