Question

Which is an irrational number?​

Answer 1

[sqrt]\sqrt{15}[/tex] is irrational.

Explanation:

Anything that can be written as a fraction where the numerator and denominator are integers is rational.

So any real number that isn't rational is irrational.

[Note:

Terminating decimals (decimals that end) can be written as fractions where numerator and denominator are integers. Therefore, terminating decimals are rational numbers.

Repeating decimals (decimals that repeat the same digit(s) at right end tail of the number) can be written as fractions where numerator and denominator are integers. Therefore, repeating decimals are rational numbers.]

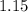`1.15` is rational because it is terminating decimal.

You can also write it as
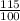`(115)/(100)`. This fraction can be reduced but the point is wrote it as an integer over an integer which is by definition a rational number.

`√(25)=5=(5)/(1)` is rational. You could say this is also a terminating decimal.

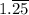`1.\overline{25}` is a repeating decimal and therefore rational.

We can write it as a fraction where numerator and denominator are integers so we can fit our formal definition of rational number.

`1.\overline{25}=1(25)/(99)=(124)/(99)`.

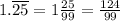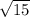`√(15)` is irrational.

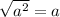`√(a^2)=a` if
`a\ge0`.

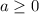Since 15 isn't a perfect square, there is no rational number that will equal
`√(15)`.

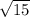The following are examples of rational numbers in this form:

`√(25)=5`

`√(16)=4`

`√(0.25)=0.5`

`√(0.16)=0.4`

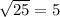
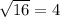
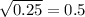
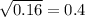
The list can be continued.

Answer 2

the first one, because it cannot be represented as a/b.