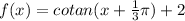Answer:
Problem 13)

Problem 14)
Explanation:
Recall how transformations affect the graph of the sine function, and how such is conveyed into the parameters A, B, C, and D that could be included in the general form of the function:
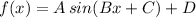
where the Amplitude of the transformed sine function is the absolute value of the multiplicative parameter A:
Amplitude =

The period is (which for sin(x) is
 ) is modified by the parameter B in the following manner:
) is modified by the parameter B in the following manner:
Period =
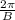
Where the phase shift is introduced as:
Phase shift =
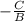 .
.
and finally any vertical shift is included by the constant D (positive means shift upwards in D many units, and negative means shift downwards D units)
Therefore, to have a sine function with the requested characteristics, we work on the value of the parameters A, B, C, and D one at a time:
1) Amplitude =
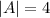 then we use parameter A = 4
then we use parameter A = 4
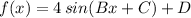
2) Period
 , then we work on the parameter B:
, then we work on the parameter B:
Period =
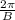
 which transforms the function into:
which transforms the function into:
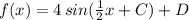
3) phase-shift =
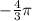
Then knowing that B=
 , we work on the value of parameter C:
, we work on the value of parameter C:
Phase shift =
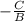
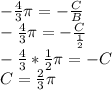
Therefore the function gets transformed into:
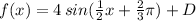
4) and finally the vertical shift of negative two units, that gives us the value D = -2
The complete transformed function becomes:

Now for problem 14, recall that the cotangent function is the reciprocal of the tangent function, therefore, their periodicity is the same:

since you are asked for a cotangent function of period
 as well, there is no multiplication parameter "B" needed (so we keep it unchanged - equal to one). B = 1
as well, there is no multiplication parameter "B" needed (so we keep it unchanged - equal to one). B = 1
Then for the phase-shift which we want it to be
 , we set the condition:
, we set the condition:
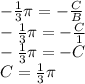
And insert such in the cotangent general form:
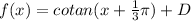
and finally include the desired vertical shift of 2 units: