Answer:
I have a lot of factors mentioned at the end of this explanation.
Explanation:
 is a difference of squares since we can write it as
is a difference of squares since we can write it as
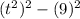 .
.
A difference of squares,
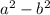 , can be factored as
, can be factored as
 .
.

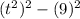
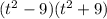
We see another difference of squares in this factored form.
I'm speaking of
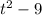 .
.
This can be rewritten as
 .
.
Let's factor it now.
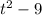

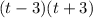
So
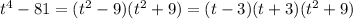 .
.
Now
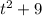 can also be factored if you invite all complex numbers into play.
can also be factored if you invite all complex numbers into play.
You will need
 here.
here.
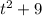

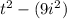
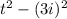
Now it is a difference of squares and we can do as we have been doing with the other factors:

So the complete factored form of
 is:
is:
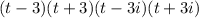 .
.
So here are some things that you could say is a factor of
 :
:

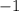
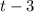
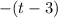
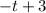 (same as one before; just a rewrite)
(same as one before; just a rewrite)
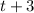
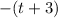
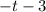 (same as one before; just a rewrite)
(same as one before; just a rewrite)
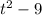
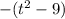
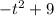 (same as one before; just a rewrite)
(same as one before; just a rewrite)
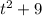
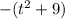
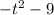 (same as one before; just a rewrite)
(same as one before; just a rewrite)

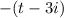
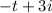 (same as one before; just a rewrite)
(same as one before; just a rewrite)
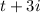
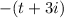
 (same as one before; just a rewrite)
(same as one before; just a rewrite)
There are other ways to write some of these hopefully you can catch them on your own in your choice if they so occur.