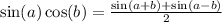Answer:
The work is in the explanation.
Explanation:
The sine addition identity is:
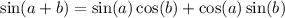 .
.
The sine difference identity is:
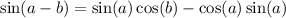 .
.
The cosine addition identity is:
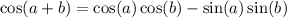 .
.
The cosine difference identity is:
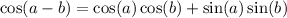 .
.
We need to find a way to put some or all of these together to get:
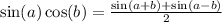 .
.
So I do notice on the right hand side the
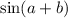 and the
and the
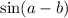 .
.
Let's start there then.
There is a plus sign in between them so let's add those together:
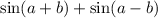
![=[\sin(a+b)]+[\sin(a-b)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/8op8jnaqnxf122h4za5atk6bufihaif8kt.png)
![=[\sin(a)\cos(b)+\cos(a)\sin(b)]+[\sin(a)\cos(b)-\cos(a)\sin(b)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/dnatx10zhfzzgrvm4hp0ticb1xs7jeqebi.png)
There are two pairs of like terms. I will gather them together so you can see it more clearly:
![=[\sin(a)\cos(b)+\sin(a)\cos(b)]+[\cos(a)\sin(b)-\cos(a)\sin(b)]](https://img.qammunity.org/2020/formulas/mathematics/middle-school/lc1hg9gnio0eps493s7rogc74sem57s1wc.png)

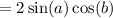
So this implies:
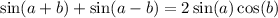
Divide both sides by 2:

By the symmetric property we can write: