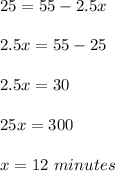Question

A rain barrel is full of water and used to water a garden. The rain barrel loses water at the rate of 2.5 gallons per minute. After seven minutes, the rain barrel contains 37.5 gallons. Part A: How many gallons of water were initially in the rain barrel? Show or explain your work. Part B: Write an equation in point-slope form to model the number of gallons (y) of water in the rain barrel after (x) minutes. show or explain your work. Part C: If the rain barrel was full of water, how many minutes does it take for the rain barrel to drain so it contains 25 gallons of water? Show or explain you work. Part D: What is the total number of minutes it will take to completely empty the rain barrel? Show or explain your work.

Answer 1

To find the number of minutes it takes for the rain barrel to completely empty, substitute 0 for y and find x.

Explanation:

0 = 55 - 2.5x

0 = 55 - 2.5x

-55 -55

-55 = -2.5x

/-2.5 /-2.5

x = 22

It takes 22 minutes to completely empty the rain barrel.

Answer 2

A. 55 gallons of water

B.
`y=55-2.5x`

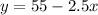
C. 12 miinutes

Explanation:

The rain barrel loses water at the rate of 2.5 gallons per minute.

Part A. After seven minutes, the rain barrel contains 37.5 gallons. During those seven minutes, the barrel loses 2.5 gallons per minute, so it loses

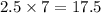`2.5* 7=17.5` gallons in 7 minutes.

Therefore, initially, there were

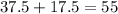`37.5+17.5=55` gallons of water.

Part B.

The slope is m = -2.5 (the barrel loses water, so the slope is negative).

Initially there were 55 gallons of water.

Hence, the equation in point-slope form to model the number of gallons (y) of water in the rain barrel after (x) minutes is

`y=55-2.5x`

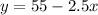
Part C.

To find the number of minutes it takes for the rain barrel to drain so it contains 25 gallons of water, substitute y = 25 and find x:

`25=55-2.5x\\ \\2.5x=55-25\\ \\2.5x=30\\ \\25x=300\\ \\x=12\ minutes`