Question

a university has found that 20% of its withdraw without copleting the courses. assume that 6 students have registered for the course the semester. compute the probability that two or fewer will withdraw, the probability that exactly four withdraw, the expected number of withdrawals, the variance for the number of withdrawals and the standard deviation for the number of withdrawals?

Answer 1

The probability that two or fewer will withdraw is 0.90112

The probability that exactly four withdraw is 0.01536

The expected number of withdrawals is 1.8

The variance for the number of withdrawals is 0.96

The standard deviation for the number of withdrawals is 0.979

Step-by-step explanation:

Binomial Distribution

It's a discrete probability distribution in which there is a number n of trials, each one with an individual probability of success p, and we want to know the probability of getting k successes.

The PMF (Probability Mass Function) is

`F(k,n,p)=\binom{n}{k}p^kq^(n-k)`

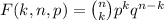
Where
`q = 1-p`

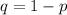
The expected value is given by

`E=np`

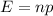
The variance can be computed with the formula

`\sigma^2=npq`

And the stardard deviation is the square root of the variance

`\sigma=√(npq)`

The university has found that 20% (p=0.20) of its students withdraw without completing the courses. Given a number of n=6 students, we must compute the following

(a) The probability that two or fewer will withdraw

The required probability will be the sum of these cases: Two studens, one student or no students will withdraw. We must compute and sum

`P(A)=F(2,6,0.2)+F(1,6,0.2)+F(0,6,0.2)`

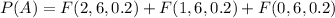
Using the PMF, and knowing q=1-p=0.8:

`\displaystyle F(2,6,0.2)=\binom{6}{2}0.2^2 0.8^(4)`

`F(2,6,0.2)=0.24576`

`\displaystyle F(1,6,0.2)=\binom{6}{1}0.2^1 0.8^(5)`

`F(1,6,0.2)=0.393216`

`\displaystyle F(0,6,0.2)=\binom{6}{0}0.2^0 0.8^(6)`

`F(0,6,0.2)=0.262144`

`P(A)=0.24576+0.393216+0.262144=0.90112`

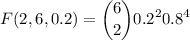
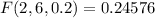
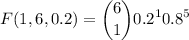
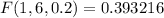
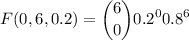
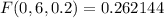
(b) The probability that exactly four withdraw. It means computing the probability when k=4

`\displaystyle F(4,6,0.2)=\binom{6}{4}0.2^4 0.8^(2)=0.01536`

`P(B)=0.01536`

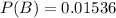
(c) The expected number of withdrawals is

`E=np=(6)(0.2)=1.8`

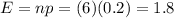
(d) The variance for the number of withdrawals is computed by

`\sigma^2=(6)(0.2)(0.8)=0.96`

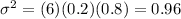
(e) The standard deviation is

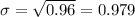`\sigma=√(0.96)=0.979`9