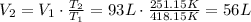Question

A 93-L sample of dry air is cooled from 145 oC to -22 oC at a constant pressure of 2.85 atmospheres). What is the final volume?

Answer 1

56 L

Step-by-step explanation:

We're dealing with a gas in this problem. We may, therefore, apply the ideal gas law for this problem:

`pV = nRT`

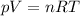
We now that we have a constant pressure. Besides, R, the ideal gas law constant, is also a constant number. Let's rearrange the equation so that we have all constant variables on the right and all changing variables on the left:

`(V)/(T) = (nR)/(p) = const`

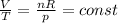
This means the ratio between volume and temperature is a constant number. For two conditions:

`(V_1)/(T_1) = (V_2)/(T_2)`

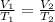
Given initial volume of:

`V_1 = 93 L`

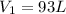
Convert the initial temperature into Kelvin:

`T_1 = 145^oC + 273.15 K = 418.15 K`

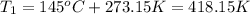
Convert the final temperature into Kelvin:

`T_2 = -22^oC + 273.15 K = 251.15 K`

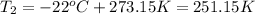
Rearrange the equation for the final volume:

`V_2 = V_1 \cdot (T_2)/(T_1) = 93 L\cdot (251.15 K)/(418.15 K) = 56 L`