Question

. At time t the displacement from equilibrium, y(t), of an undamped spring-mass system of mass m is governed by the initial-value problem den nye+w+y = Fo coswt, y0) = 1, diy (0) = 0 та where Fo and w are positive constants. Solve this initial value problem to determine the motion of the system. What happens as t o

Answer 1

a)
`y(t) =cos (\omega t)`

b) As t →∞ y(t) becomes undefined as value of cos is undefined at ∞

Explanation:

Considering the complete question attached in fig below:

Non-homogeneous differential equation for given undamped system is:

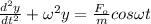`(d^(2)y)/(dt^2) + \omega ^2y = (F_(o))/(m) cos \omega t` ---(1)

To find general solution, consider the homogeneous part:

`(d^(2)y)/(dt^2) + \omega ^(2)y =0\\\implies D^2+\omega =0\\\implies D=\pm \omega i`

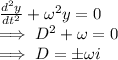
General solution is

`y_(h) = A cos \omega t + B sin \omega t`

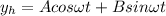
Using method of undetermined co-efficient,find the particular solution:

`y_(p) = (F_(o))/(m) (c_(1) cos \omega t +c_(2) sin \omega t)\\y'_(p) = (F_(o))/(m) \omega (-c_(1) sin \omega t +c_(2) cos \omega t)\\y''_(p) = (F_(o))/(m) \omega^(2) (-c_(1) cos \omega t-c_(2) sin \omega t)`

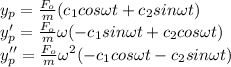
Substituting all these values in (1)

`-(F_(o))/(m) \omega^(2) (c_(1) cos \omega t+c_(2) sin \omega t) + \omega^(2)(c_(1) cos \omega t+c_(2) sin \omega t) =-(F_(o))/(m) cos\omega t`

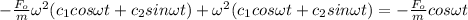
Equating the terms on both sides

`\omega^2 cos \omega t (-(F_(o))/(m)+1) c_(1) = (F_(o))/(m) cos \omega t\\\omega^2sin \omega t (-(F_(o))/(m) +1) c_(2)=0\\\implies c_(2) =0`
`c_(1) = (F_(o))/(\omega^2 (-F_(o) +m))`

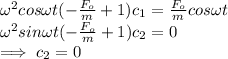
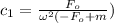
solution of given differential eq. :

`y(t) =y_(h) + y_(p)\\y(t) = A cos \omega t + B sin \omega t +c_1 cos \omega t -----(2)\\y'(t) = \omega (-A sin \omega t + B cos \omega t - c_1 sin \omega t`

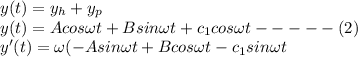
Using initial values :

`y(0) = A cos \omega (0) + B sin \omega (0_ +c_1 cos \omega (0)\\1 = A + c_1\\A = 1 -c_1\\y'(0) = \omega (-A sin \omega (0) + B cos \omega (0) - c_1 sin \omega (0)\\B= 0`

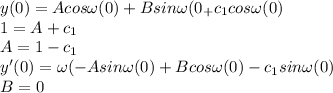
then (2) becomes

`y(t) = A cos ( \omega t) + c_1 cos (\omega t)\\y(t) = (1- c_1)cos ( \omega t) + c_1 cos (\omega t)`

`y(t) =cos (\omega t)`

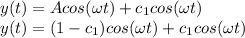
As t →∞

y(t) becomes undefined as value of cos is undefined at ∞