Question

BH+ClO4- is a salt formed from the base B (Kb = 1.00e-4) and perchloric acid. It dissociates into BH+, a weak acid, and ClO4-, which is neither an acid nor a base. Find the pH of 0.100 M BH+ClO4-.

Answer 1

The pH of 0.1 M BH⁺ClO₄⁻ solution is 5.44

Step-by-step explanation:

Given: The base dissociation constant:
`K_(b)` = 1 × 10⁻⁴, Concentration of salt: BH⁺ClO₄⁻ = 0.1 M

Also, water dissociation constant:
`K_(w)` = 1 × 10⁻¹⁴

The acid dissociation constant (
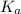`K_(a)`) for the weak acid (BH⁺) can be calculated by the equation:

`K_(a). K_(b) = K_(w)`

`\Rightarrow K_(a) = (K_(w))/(K_(b))`

`\Rightarrow K_(a) = (1* 10^(-14))/(1* 10^(-4)) = 1* 10^(-10)`

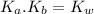
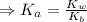
Now, the acid dissociation reaction for the weak acid (BH⁺) and the initial concentration and concentration at equilibrium is given as:

Reaction involved: BH⁺ + H₂O ⇌ B + H₃O+

Initial: 0.1 M x x

Change: -x +x +x

Equilibrium: 0.1 - x x x

The acid dissociation constant:
`K_(a) = (\left [B \right ] \left [H_(3)O^(+)\right ])/(\left [BH^(+) \right ]) = ((x)(x))/((0.1 - x)) = (x^(2))/(0.1 - x)`

`\Rightarrow K_(a) = (x^(2))/(0.1 - x)`

`\Rightarrow 1* 10^(-10) = (x^(2))/(0.1 - x)`

`As, x << 0.1`

`\Rightarrow 0.1 - x = 0.1`

`\therefore 1* 10^(-10) = (x^(2))/(0.1 )`

`\Rightarrow x^(2) = (1* 10^(-10))* 0.1 = 1* 10^(-11)`

`\Rightarrow x = \sqrt{1* 10^(-11)} = 3.16 * 10^(-6)`

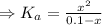
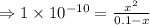
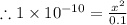
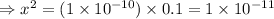
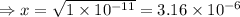
Therefore, the concentration of hydrogen ion: x = 3.6 × 10⁻⁶ M

Now, pH = - ㏒ [H⁺] = - ㏒ (3.6 × 10⁻⁶ M) = 5.44

Therefore, the pH of 0.1 M BH⁺ClO₄⁻ solution is 5.44