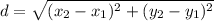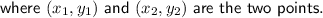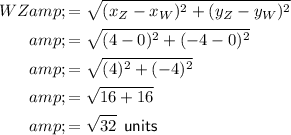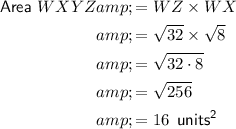Answer:
1. 17.5 units²
2. 16 units²
Explanation:
Question 1
Given vertices of ΔABC:
- A = (-3, 2)
- B = (4, 2)
- C = (4, -3)
Plot the vertices on the given graph paper and join with line segments to create the triangle.
As point B and C share the same x-coordinate, and points A and B share the same y-coordinate, ΔABC is a right triangle with base AB and height BC.
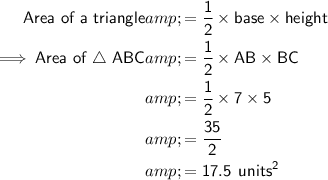
Question 2
Given vertices of rectangle WXYZ:
- W = (0, 0)
- X = (2, 2)
- Y = (6, -2)
- Z = (4, -4)
Plot the vertices on the given graph paper and join with line segments to create the rectangle.
The area of a rectangle is found by multiplying the length by the width. To find the area of rectangle WXYZ, find the length (WZ or XY) and the width (WX or ZY) using the distance formula, then multiply them.
Distance between two points