Question

A communications satellite with a mass of 420 kg is in a circular orbit about the Earth. The radius of the orbit is 2.9×10^4 km as measured from the center of the Earth. Calculate (a) the weight of the satelitte on the surface of the earth and (b) the gravitational force exerted on the satellite by the Earth when it is in orbit.

Answer 1

To solve this problem we will apply the concepts related to Newton's second law that will allow us to find the Weight of the object, and the law of universal gravitation raised by it, in order to find it at a certain point.

Part A) We know the acceleration due to gravity on the surface:

F=m*a

Where,

m = mass

a = Gravitational acceleration

`F_w = 420*9.81`

`F_w=4120.2N`

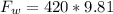
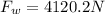
Therefore the weight of the satellite on the surface of the earth is 4.1kN

Part B) To find the acceleration due to gravity at 29*10^3 km above the earth's center, we need to use Newton's law of universal gravitation:

`W_g = (GMm)/(r^2)`

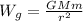
Where,

G = Gravitational universal constant

M = Mass of Earth

m = Mass of the object

r = Distance from center of Earth

Replacing,

`W_g = ((6.67*10^(-11))(5.97*10^(24))(420))/((29*10^6)^2)`

`W_g =198.8627N`

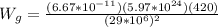
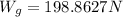
Therefore the gravitational force exerted on the satellite by the Earth when it is in orbit is 198.8N