What is the sum of all positive integers smaller than $1000$ that can be written in the form $100\cdot 2^n$, where $n$ is an integer (not necessarily positive)

Question

asked Dec 7, 2020 133k views

1 Answer

Epotter · Answer 1 · 2020-12-13T10:27:17+0000

Answer:

The sum is 1575.

Explanation:

Consider the provided information.

It is given that positive integers smaller than 1000 and that can be written in the form
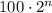
$100\cdot 2^n$

Where n is integer that means the value of n can be a positive number or a negative number.

For n = 0

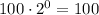
$100\cdot 2^(0)=100$

For n=-1

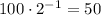
$100\cdot 2^(-1)=50$

For n=-2

$100\cdot 2^(-2)=25$

For n = -3 the obtained number is not an integer.

Now consider the positive value of n.

For n=1

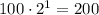
$100\cdot2^1 = 200$

For n=2

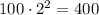
$100\cdot2^2 = 400$

For n=3

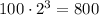
$100\cdot2^3 = 800$

For n=4 the obtained number is greater than 1000.

Now add all the numbers.

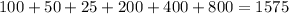
100+50+25+200+400+800=1575

Hence, the sum is 1575.