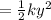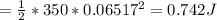Answer:
TOTAL ENERGY = 0.74 j
Step-by-step explanation:
Given data:
spring constant is 350 N/m
m = 0.24 kg
b = 0.41 kg/s
A = 0.075 M

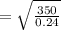
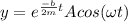
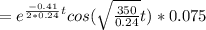
after one full cycle, mass will be at extreme point, hence K,E = 0
But total energy remain same
y after one full cycle is\
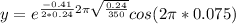
y = 0.06517 m
y = 6.517 cm
total energy