Question

A 986-kg roller coaster starts from the top of a hill and rolls down. It enters a loop for which the radius at the top is 92.5 meters. The track is designed in such a way that 4260 Newtons is the maximum force allowed in the rail.

Answer 1

20 m/s

Step-by-step explanation:

mass, m = 986 kg

radius, r = 92.5 m

maximum force, F = 4260 N

Let the velocity is v.

the force required is centripetal force.

`F=(mv^(2))/(r)`

`4260=(986* v^(2))/(92.5)`

v² = 399.65

v = 20 m/s

Thus, the maximum velocity is 20 m/s.

Answer 2

v = 20 m/s

Step-by-step explanation:

given,

mass of the roller = 986 Kg

radius = 92.5 m

maximum allowable force = 4260 N

now, calculating the maximum speed of the roller coaster = ?

now, force due to centripetal acceleration

`F = (mv^2)/(r)`

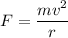
total force acting will be equal to

`F =(mv^2)/(r)`

`4260 =(986* v^2)/(92.5)`

`10.659 v^2 = 4260`

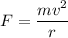
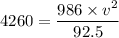
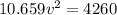
v² = 400

v = 20 m/s

hence, the maximum speed which roller coaster can attain is equal to v = 20 m/s