Question

Please help me with the following questions. Thanks in advance!

Answer 1

Explanation:

For #6, first use the rule to "undo" the division. That rule is subtraction:

`log(x^2y^6-z^3)`

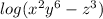
Now "undo" the multiplication with addition:

`log(x^2+y^6-z^3)`

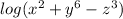
The last rule is to pull down the exponent to the front:

`log(2x+6y-3z)`

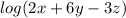
For #7, begin by setting each expression equal to x, what we are solving for.

`log_(4)18=x`

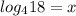
Writing this as an exponent:

`4^x=18`

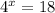
Take the natural log of both sides:

`ln(4^x)=ln(18)`

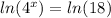
Following the same rule as above, we can pull the x down front:

x ln(4)= ln(18)

To solve for x, just divide both sides by ln(4) to get that

x = 2.08

Do the same thing for 7b.

`log_{(1)/(2) }74=x` and

`(1)/(2)^x=74` and

`ln((1)/(2))^x=ln(74)` and

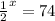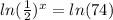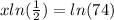`xln((1)/(2))=ln(74)` and divide both sides by ln(1/2) to get that

x = -6.21