Question

A non-conducting sphere of radius R = 3.0 cm carries a charge Q = 2.0 mC distributed uniformly throughout its volume. At what distance, measured from the center of the sphere, does the electric field reach a value equal to half its maximum value?a. 1.5 cm and 2.1 cmb. 1.5 cm onlyc. 2.1 cm onlyd. 1.5 cm and 4.2 cme. 4.2 cm only

Answer 1

To solve this problem we will use the concept of electric field, with which we will make the proportional comparison as we move away from the center. So we have the maximum electric field is given as,

`E_(max) = (kQ)/(R^2)`

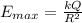
Where,

Q = Charge

R = Radius

Electric field inside the sphere is given as,

`(kQ)/(R^2) = (1)/(2)(kQ)/(R^2)`

`R'=√(2)R`

`R' = 3√(2)`

`R' = 4.2cm`

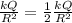
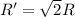
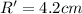
Electric field outside the sphere is given as,

`(kQ)/(2R^2) = (1)/(2)(kQ)/(R^3)r`

`(1)/(2) = (r')/(R)`

`\Rightarrow (R)/(2) = (3)/(2) = 1.5cm`

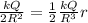
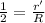
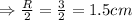
Therefore the possible values are 3.5cm and 9.9cm: The correct answer is D.