Question

A 35 kg trunk is pushed 4.8 m at constant speed up a 30° incline by a constant horizontal force. The coefficient of kinetic friction between the trunk and the incline is 0.19.

Calculate the work done by the applied horizontal force.
Calculate the work done by the weight of the trunk.
How much energy was dissipated by the frictional force acting on the trunk?
From now suppose the 35 kg trunk is pushed 4.8 m at constant speed up a 30° incline by a force along the plane (not as in the figure). The coefficient of kinetic friction between the trunk and the incline is 0.19.
Calculate the work done by the applied force.
Calculate the work done by the weight of the trunk.
How much energy was dissipated by the frictional force acting on the trunk?

Answer 1

The work done by a horizontal force on a trunk up an incline involves several factors, including force magnitude, displacement, angle of application, and the energy dissipated by friction depends on the distance and the coefficient of kinetic friction.

Step-by-step explanation:

To calculate the work done by the applied horizontal force when pushing the trunk up the incline, we must consider the displacement, the angle of the applied force relative to the direction of displacement, and the magnitude of the force. The work done by the weight of the trunk involves the vertical displacement, which can be found using trigonometry and the gravitational force. The energy dissipated by the frictional force, on the other hand, involves the coefficient of kinetic friction, the normal force, and the distance traveled. When the force is applied along the incline rather than horizontally, the work done by the applied force involves the component of the force parallel to the incline and the distance moved.

For the horizontal force, the work done by the weight and the energy dissipated by friction would remain the same as the previous scenario since they are dependent on the properties of the incline and the trunk itself.

Answer 2

We need to separate the x- and y-components of the applied force. For simplicity, I will denote the direction along the inclined plane as x-direction, and the perpendicular direction as y-direction.

`F_x = F\cos(30^\circ)\\F_y = F\sin(30^\circ)`

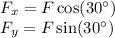
Only the x-component of the applied horizontal force does work on the trunk.

But we need to find the magnitude of the force. We know that the trunk is moving with constant speed. So, the x-component of the applied force is equal to the x-component of the gravitational force plus the force of friction.

`0 = F\cos(30^\circ) - mg\sin(30^\circ) - mg\cos(30^\circ)\mu\\0.86F = 35(9.8)(0.5) + 35(9.8)(0.86)(0.19)\\F =264.5N`

`F_x = 264.5\cos(30^\circ) = 227.5N\\F_y = 264.5\sin(30^\circ) = 132.25N`

`W_(F_x) = F_xd = 227.5* 4.8 = 1092J`

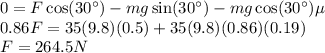
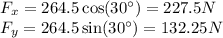
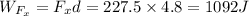
The work done by the weight of the trunk can be calculated similarly. Only the x-component of the weight does work on the trunk.

`W_g = -mg\sin(30^\circ)d`

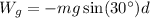
Note that the direction of the weight force is opposite of the direction of the motion, so this force does negative work on the trunk.

`W_g = -823J`

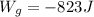
The energy dissipated by the frictional force can be found as follows:

`W_f = -mg\cos(30^\circ)\mu d = -35(9.8)(0.86)(0.19)(4.8) = -269J`

Additionally, the sum of work done by the friction and weight is equal in magnitude to the work done by the applied force. This shows that our calculations are consistent.

In the second part of the question, the applied force is on the x-direction. We will follow a similar procedure but a different force.

`0 = F - mg\sin(30^\circ) - mg\cos(30^\circ)\mu\\0 = F - 35(9.8)(0.5) - 35(9.8)(0.86)(0.19)\\0 = F - 171.5 - 56\\F = 227.5N`

`W_F = Fd = 227.5* 4.8 = 1092J`

`W_g = -mg\sin(30^\circ)d = -35(9.8)(0.5)(4.8) = -823J`

`W_f = -mg\cos(30^\circ)\mu d = -35(9.8)(0.86)(0.19)(4.8) = -269J`

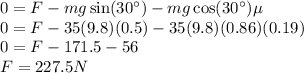
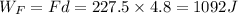
Explanation:

As you can see above, the answers are the same, although the directions of the applied forces are different. The reason for this situation is that in the first part the y-component does no work.