Question

A container with 0.389 L of water is placed in a microwave and radiated with electromagnetic energy with a wavelength of 12.9 cm. The temperature of the water rose by 78.7 °C. Calculate the number of photons that were absorbed by the water. Assume water has a density of 1.00 g ⋅ mL − 1 and a specific heat of 4.184 J ⋅ g − 1 ⋅ ° C − 1 .

Answer 1

Step-by-step explanation:

The given data is as follows.

V = 0.389 L = 0.389 kg

m = 389 g of water (as 1 kg = 1000 g)

wavelength = 12.9 cm

dT =
`78.7^(o)C`

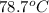
First, we will identify the heat absorbed as follows.

Q =
`m * C * (T_(f) - T_(i))`

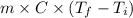
Putting the given values into the above formula as follows.

Q =
`m * C * (T_(f) - T_(i))`

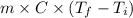
Q =
`389 g * 4.184 * (78.7^(o)C)`

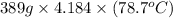
= 128090.231 J

Now, as we know that

Energy (E) =
`(hc)/(\lambda)`

or,
`\lambda = (hc)/(E)`

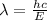
where, h = Planck's Constant =
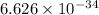`6.626 * 10^(-34)` J s

c = speed of particle (i.e. light) =
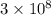`3 * 10^(8)` m/s

E = energy per particle J/photon

Hence, calculate the energy as follows.

E =
`(6.626 * 10^(-34) * 3 * 10^(8))/(0.129 m)`

(As 1 m = 100 cm)

=
`1.5409 * 10^(-24)` J/photons

Hence, number of photons present will be calculated as follows.

n photons =
`(Q)/(E)`

=
`(128090.231 J)/(1.5409 * 10^(-24))`

=
`83126.89 * 10^(24)`

=
`8.312 * 10^(28)`

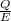
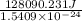
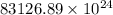
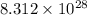
Thus, we can conclude that number of photons released are
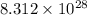`8.312 * 10^(28)`.