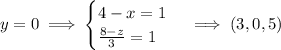The line has equation
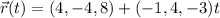
where
 is any real number.
is any real number.
 is the line containing all scalar multiples of the vector (-1, 4, -3); we add (4, -4, 8) to shift the line so that it passes through this point while remaining parallel to the the line.
is the line containing all scalar multiples of the vector (-1, 4, -3); we add (4, -4, 8) to shift the line so that it passes through this point while remaining parallel to the the line.
To get the symmetric form, we have
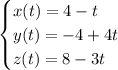
Solving for
 in each equation gives the symmetric form,
in each equation gives the symmetric form,
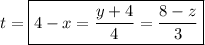
The line has intercepts in the coordinate planes wherever either the
 ,
,
 , or
, or
 coordinate is 0.
coordinate is 0.
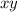 -plane:
-plane:
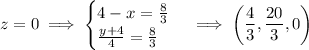
 -plane:
-plane:
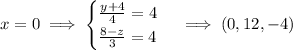
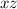 -plane:
-plane: