Question

Boiling water at 100℃ is placed in a freezer at 0℃. The temperature of the water is 50℃ after 24 minutes. Approximate the temperature of the water after 96 minutes.

Answer 1

Therefore, the temperature of the water after 96 min (5760 s) = 279.25 K = 6.25 ℃

Step-by-step explanation:

Given: Time: t₁ = 24 min = 24 × 60 s = 1440 s

Time: t₂ = 96 min = 96 × 60 s = 5760 s (∵ 1 min = 60 s)

Initial Temperature of the water: T(0) = 100℃ = 100 + 273 K = 373 K

Ambient temperature (temp of the freezer): Tₐ = 0℃ = 0 + 273 K = 273 K

Temperature of the water at time t₁: T(t₁) = 50℃ = 50 + 273 K = 323 K

(∵ 0℃ = 273 K)

Temperature of the water at time t₂: T(t₂) = ? K

According to the Newton's Law of Cooling:

`[T(t) - T_(a)] = [T(0) - T_(a)] e^(-kt)`

Here, k is the cooling constant

`\therefore [T(t_(1)) - T_(a)] = [T(0) - T_(a)] e^{-kt_(1)}`

`\Rightarrow [323\, K - 273\, K] = [373\, K - 273\, K] e^(-k(1440 sec))`

`\Rightarrow [50] = [100] e^(-k(1440 sec))`

`\Rightarrow 0.5 = e^(-k(1440 sec))`

`\Rightarrow ln(0.5)= -k * 1440`

`\Rightarrow (-0.69)= -k * 1440`

`\Rightarrow The\, cooling\, constant:\, k = 0.00048\, s^(-1)`

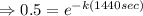
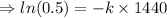
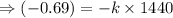
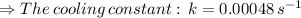
Now to find the temperature of water at time: t₂, we use the equation:

`[T(t_(2)) - T_(a)] = [T(0) - T_(a)] e^{-kt_(2)}`

`\Rightarrow [T(t_(2)) - 273\, K] = [373\, K - 273\, K] e^{-(0.00048\, s^(-1))(5760\, s)}`

`\Rightarrow [T(t_(2)) - 273] = [100] e^(-2.7726)`

`\Rightarrow [T(t_(2)) - 273] = 100 * 0.0625`

`\Rightarrow [T(t_(2)) - 273] = 6.25`

`\Rightarrow T(t_(2)) = 273 + 6.25 = 279.25\, K`

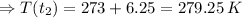
∵ 0℃ = 273 K

∴ T(t₂) = 279.25 K = 279.25 - 273 ℃ = 6.25 ℃

Therefore, the temperature of the water after 96 min (5760 s) = 279.25 K = 6.25 ℃