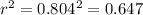Answer:
1)
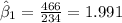
2)

3)
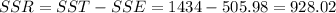
4)
![r=(466)/(√([234][\sum(1434]))=0.804](https://img.qammunity.org/2020/formulas/mathematics/college/i0rdugpyws2ku0q8jmugyjjjalu55snnks.png)
And the determination coeffecient is
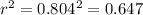
Explanation:
The correlation coefficient is a "statistical measure that calculates the strength of the relationship between the relative movements of two variables". It's denoted by r and its always between -1 and 1.
The sum of squares "is the sum of the square of variation, where variation is defined as the spread between each individual value and the grand mean"
When we conduct a multiple regression we want to know about the relationship between several independent or predictor variables and a dependent or criterion variable.
Data given
n=10

Part 1
The slope is given by this formula:
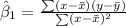
If we replace we got:
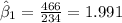
Part 2
We can find the intercept with the following formula
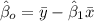
We can find the average for x and y like this:
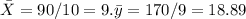
And replacing we got:

Part 3
For this case we have the SSE=505.98 who represent the sum of squares for the error.
The total sum of squares is given by
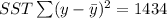
And since the total variation is the sum of squares for the regression and the error we have this:
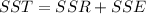
And solving for SSR we got:
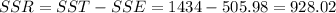
Part 4
In order to calculate the correlation coefficient we can use this formula:
![r=(\sum (x-\bar x)(y-\bar y) )/(√([\sum (x-\bar x)^2][\sum(y-\bar y)^2]))](https://img.qammunity.org/2020/formulas/mathematics/college/gmvz1y7e3a2nylrbaymej8ngsma850u7ay.png)
For our case we have this:
n=10

So we can find the correlation coefficient replacing like this:
![r=(466)/(√([234][\sum(1434]))=0.804](https://img.qammunity.org/2020/formulas/mathematics/college/i0rdugpyws2ku0q8jmugyjjjalu55snnks.png)
And the determination coeffecient is