Question

A wad of clay with a mass, m, of 1.5 kg is initially moving with a horizontal velocity of 3 m/s when it strikes and sticks to an initially stationary uniform slender bar with a mass of 11 kg (M) and total length, L, of 7 m. Determine:

Answer 1

To solve this question, we need to know the angle and the position at which the clay hits the bar. I will denote the angle as ∅ and the position from the pivot as 'r'.

We will use the conservation of angular momentum.

`L_1 = L_2\\mvr\sin(\phi) = I\omega\\mvr\sin(\phi) = ((1)/(3)ML^2 + mr^2)\omega\\(1.5)(3)(r)\sin(\phi) = ((1)/(3)(11)(7)^2  + (1.5)(r)^2)\omega\\\omega = (4.5r\sin(\phi))/(179.6 + 1.5r^2)`

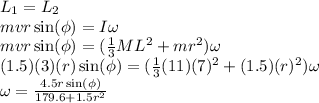
The linear impulse is equal to the change in the linear momentum. The horizontal component of the angular momentum is calculated above. The vertical component of the initial angular momentum is ineffective, because its torque is zero. However, the linear impulse can be calculated.

`\vec{J} = \vec{P}_2 - \vec{P}_1\\\vec{J} = 0 - mv\cos(\phi)\\\vec{J} = -4.5\cos(\phi)`

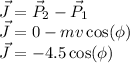
Step-by-step explanation:

After the collision both masses are combine, so the moment of inertia of the combined object can be calculated by adding the moment of inertia of both objects.