Question

A satellite is in circular orbit at an altitude of 1500 km above the surface of a nonrotating planet with an orbital speed of 9.2 km/s. The minimum speed needed to escape from the surface of the planet is 14.9 km/s, and G = 6.67 × 10-11 N · m2/kg2. The orbital period of the satellite is closest to

Answer 1

To solve this problem we will use the Newtonian theory about the speed of a body in space for which the speed of a body in the orbit of a planet is summarized as:

`v =  \sqrt{(2GM)/(R)}`

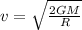
Where,

G = Gravitational Universal Constant

M = Mass of Planet

r = Radius of the planet ('h' would be the orbit from the surface)

The escape velocity is

`v = 14.9km/h = 14900m/s`

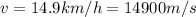
Through this equation we can find the mass of the Planet in function of the distance, therefore

`M = (v^2R)/(2G)`

`M = (14900^2R)/(2(6.67*10^(-11)))`

`M = 16.64*10^(17)R`

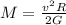
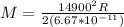
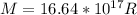
The orbital velocity is

`v_o = \sqrt{(GM)/(R+h)}`

`9200^2 = ((6.67*10^(-11))(16.64*10^(17))R)/(R+1500*10^3)`

`11.1*10^7R = (R+15000*10^3)(9200)^2`

`2.64*10^7R = 12.69*10^(13)`

`R = 4.81*10^6m`

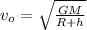
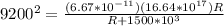
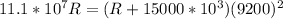
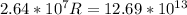
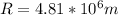
The time period of revolution is,

`T = (2\pi(R+h))/(v_o)`

`T = (2\pi(4.81*10^6+1.5*10^6))/(9200)`

`T = 4307s`

`T = 72min = 1hour12min`

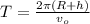
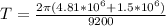
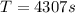
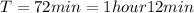
Therefore the orbital period of the satellite is closes to 1 hour and 12 min