Question

You are standing 30 m from a window that is 30 m off the ground. Your friend tries to toss you something, but only throws it straight up. If you start from rest and have a maximum acceleration of 2m/s^2, what is the minimum initial velocity that your friend could have thrown the object to enable you to catch it?

Answer 1

The minimum initial velocity is 21.37 m/s.

Step-by-step explanation:

Given that,

Distance = 30 m

Acceleration = 2 m/s²

We need to calculate the time

Using equation of motion

`s=ut+(1)/(2)at^2`

`t=\sqrt{(2s)/(a)}`

Put the value into the formula

`t=\sqrt{(2*30)/(2)}`

`t=5.48\ sec`

We need to calculate the minimum initial velocity

Again using second equation of motion

`-s=ut-(1)/(2)gt^2`

Put the value into the formula

`-30=u*5.48-(1)/(2)*9.8*(5.48)^2`

`u=((1)/(2)*9.8*(5.48)^2-30)/(5.48)`

`u=21.37\ m/s`

Hence, The minimum initial velocity is 21.37 m/s.

Answer 2

minimum initial velocity is 21.35 m/s

Step-by-step explanation:

given data

distance S = 30 m

height h = 30 m

maximum acceleration a = 2 m/s²

to find out

minimum initial velocity that your friend could have thrown the object to enable you to catch

solution

first we get here time with the help of second equation of motion

time =
`\sqrt{(2h)/(a) }` ..................1

put her value we get

time =
`\sqrt{(2*30)/(2) }`

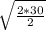
time = 5.477 second

and that is time which tossed object must be take so we apply here again second equation of motion that is

-S = ut - 0.5 × gt² .......................2

-30 = u× 5.477 - 0.5 ×9.8×5.477²

solve it we get

u = 21.35 m/s

so minimum initial velocity is 21.35 m/s