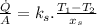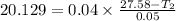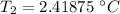Answer:
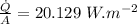
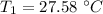 &
&
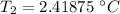
Step-by-step explanation:
Given:
- interior temperature of box,
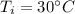
- height of the walls of box,
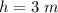
- thickness of each layer of bi-layered plywood,
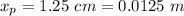
- thermal conductivity of plywood,
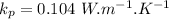
- thickness of sandwiched Styrofoam,
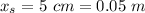
- thermal conductivity of Styrofoam,
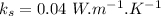
- exterior temperature,
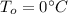
From the Fourier's law of conduction:
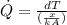
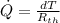 ....................................(1)
....................................(1)
Now calculating the equivalent thermal resistance for conductivity using electrical analogy:
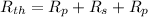
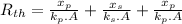
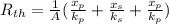
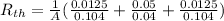
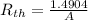 .....................(2)
.....................(2)
Putting the value from (2) into (1):
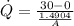
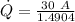
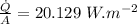 is the heat per unit area of the wall.
is the heat per unit area of the wall.
The heat flux remains constant because the area is constant.
For plywood-Styrofoam interface from inside:
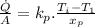
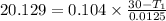
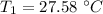
&For Styrofoam-plywood interface from inside: